The convexity bias is a technical trade-off between either a strip of STIR futures versus an interest rate swap, or in single period terms, a trade off between a single STIR future and an equivalent term forward rate agreement (FRA). A FRA is an over-the-counter bilateral product that allows the buyer /seller to notionally borrow/lend a specified amount at a LIBOR linked rate over a forward period.
What is the convexity bias?
The rationale for the convexity bias exists due to the FRA’s convex payoff compared to STIR futures linear payoff. As underlying rates move up and down, a position in STIR futures will have the same payoff but that of the FRA will change. The convexity of the FRA comes about due to its discounted payoff.
- The payoff of a short STIR future is given by (L%-F%)* 10000*$25
- The payoff of a short FRA is given by ((F%-L%)* Notional*0.25)/(1+L%*0.25)
Where
- F% is the FRA forward rate or rate implied by STIR
- L% is the FRA maturity date LIBOR rate or futures EDSP rate.
- 0.25 is the 3-month accrual (in reality measured by ACT/360 convention for USD and EUR)
- $25 assumes Eurodollar tick value per basis point.
Example:
The table shows the convexity bias between a position of short 1000 Eurodollar (ED) futures and an offsetting short $1005m 3-month FRA (slightly more than $1000m to compensate for discounting methodology), both instigated at a rate of 2%.
- An increase in underlying rates from 2% to 2.10% would result in a credit to the variation margin account of short 1000 ED STIR position of $250,000 and a debit of slightly less than that in the discounted equivalent of $1005m 3M FRA collateral account (assuming zero threshold – zero threshold means every dollar of value change has to be made good.).
- A decrease in underlying rates of 10 basis points to 1.9% would result in a debit to the variation margin account of a short 1000 ED STIR position of $250,000 and a credit of slightly more than that in the $1005m 3-month FRA collateral account (assuming zero threshold).
If the rates on both products were the same, there would be an advantage or bias in borrowing (selling) via the STIR future and lending via a short FRA to take advantage of the FRA’s convexity. This means that STIR futures should in theory trade at a higher rate compared to the equivalent term FRA. The amount of this difference is the convexity bias which is dependent on and driven by term and short rate volatility.
Monetarising the bias
The convexity bias is monetarised via margining. The short STIR future position would result in beneficial variation margin flows. If rates moved higher, the variation margin account would be credited and this could be lent out at higher overnight rates. If rates moved lower, the variation margin deficit could be financed at lower rates. Time and rate volatility would give rise to what is effectively a long gamma payoff.
Disappearing act
However, as a consequence of the financial crisis, many over-the-counter derivatives like FRA’s and swaps are migrating to an exchange traded and central counterparty cleared model, the convexity bias has largely disappeared as both products will be margined in a similar futures like way.
Furthermore, today’s low interest rate environment means that margins are subject to higher funding rates that often exceed the amounts that can be earned on margin. Also, funding margin accounts can be very capital intensive for products that don’t benefit from cross margining benefits. For example, a Euribor STIR future trade against a EUR swap/FRA might attract two sets of independent margins whereas a Eurodollar STIR future trade against a USD swap/FRA would be more capital efficient since both products are cleared by CME Group.
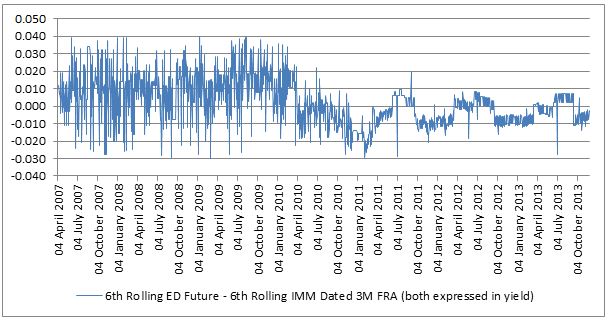
The chart shows the convexity bias that used to exist on Eurodollar futures prior to 2011, when central counterparty clearing for swaps and FRA’s gained traction. Now it has largely disappeared due to the cross margining benefit of both products being cleared and margined by CME Group.
ED Convexity bias
In Europe, the bias went slightly negative this summer mainly since margins for LIFFE Euribor futures could not be netted against margins for Euro FRA’s cleared at SwapClear. Any trader doing the European convexity bias trade would have to post two sets of margin and as the rate paid on margin is lower than the trader’s own funding costs, a substantial funding adjustment results which would be greater than value of the convexity bias. Consequently, there was nothing to prevent the bias going negative!