Roll yield is more commonly associated with the $250 billion commodity markets than STIR futures. Here, traders and fund managers replicate commodity investment and commodity indices by buying futures and rolling each (monthly ) expiry. When the commodity forward curve is backwardated (longer dated forwards < near dated forwards), there is a positive roll pick-up which is called the roll yield. This is a consequence of the long futures position being allowed to expire and the long exposure being reinstated by buying the next futures contract which is trading lower than the expiring series. Various studies have shown that roll yield has added a significant amount to commodity returns over the last couple of decades.
A couple of years ago, I wondered whether this might apply to STIR futures. Admittedly, there is a very different set of curve dynamics to that of commodity markets but there are some observable knowns:
- STIR forward curve are generally positive (longer dated futures > shorter dated futures – in yield terms).
- The nearer parts of the STIR curve are often steeper, in yield terms, than the further parts.
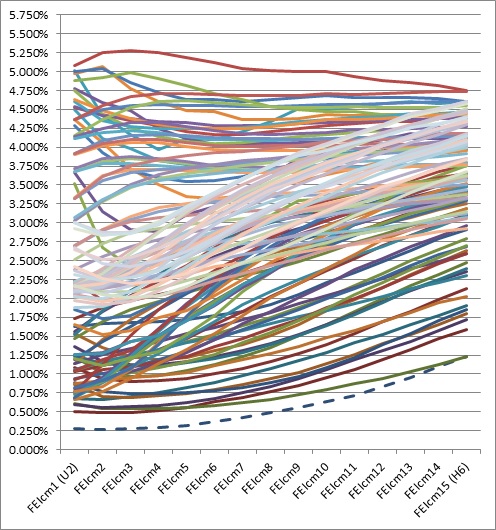
The chart below shows this generalisation – curves are usually positive but will experience prolonged periods where they are negative, usually at the perceived top of a rate cycle and/or in expectation of an economic downtown. Most of the negative curves in the chart occurred post Lehman in late 2008.
Monthly implied forward curves from LIFFE Euribor futures June 2002 to July 2012
(Dotted line – latest curve in 2012)
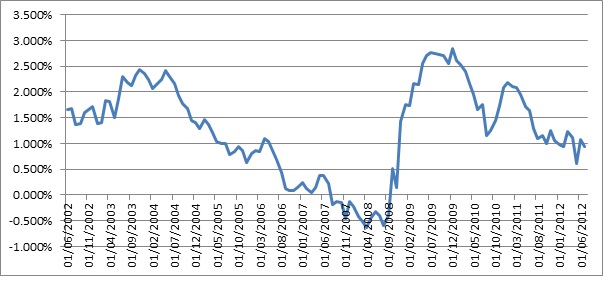
The following chart puts this in perspective.
Euribor Stir futures curve steepness 2002 – 2012
(15th quarterly expiry – 1st quarterly expiry)
(Higher value = steeper curve, Negative value = negative sloping curve)
Rather than look at the effects of instigating a rolling long or short position, like the commodity replication trades, which will be largely driven by market returns as well as roll yields, I thought it might be interesting to look at the returns on buying a 3-month spread and letting it roll down the curve. The general idea being to buy the spread where the curve is flat, in which case the purchase price should be close to zero and sell it when it has aged and rolled down the curve to a steeper point, usually closer to expiry, where it is sold, hopefully at a higher price. A spread is sold each month and so the process is on-going over time.
Based on my data sample (Dec 1999- Dec 2011), the optimised strategy was the following:
- Buy one 3M spread
- E.g. the 18th 3M spread
- Starting in December 1999, this was the M4U4 at 0.06
- Sell spread 36 months later
- M4U4 spread sold in December 2002 for 0.195
- Roll every month for 10 years
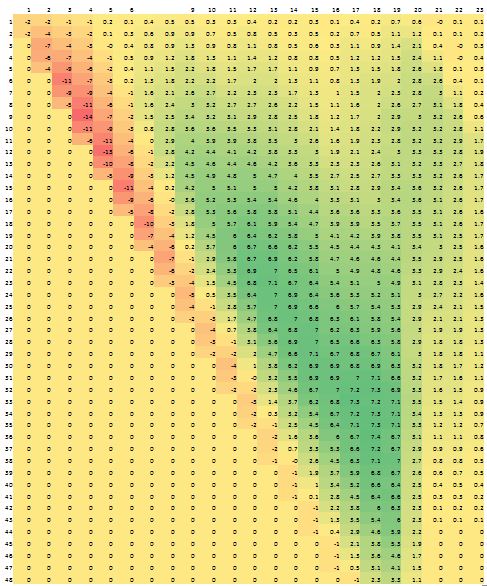
The table shows the result of the backtest.
The horizontal axis shows the Nth spread to use (1 is the front spread e.g if today is Oct 13, then Z13H14 and 2 would be H14M14) and the vertical axis is selling N months later.
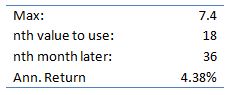
Therefore, the table shows that based upon this data sample (Dec 1999 – Dec 2011) optimal strategy to use is to buy the 18th spread along the curve and to sell it 36 months later. Such a strategy would have returned 7.4 ticks over the period representing an approximated 4.3% return on expected margin financing (fees and transaction expenses not included).
Not exactly a killing but perhaps something for a systematic trader to run with, especially one who is willing to include a bit of trading intuition to avoid periods where the curve is negative or trending towards that state.